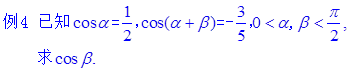课题

3.1.1两角差的余弦公式

课型

新授课

章节

人教版数学必修四第三章第一节

年级班级

高一（10）班

教学

目标

1. 知识与技能

(1)掌握两角差的余弦公式,并能用之解决简单的问题。

(2)通过对公式的推导,对学生渗透探究思想、类比思想。

2. 过程与方法目标：

 通过对公式的推导提高学生研究问题、分析问题、解决问题能力；体会公式探求中从特殊到一般的数学思想，同时渗透如上所说的多种数学思想。

3. 情感与态度目标：

通过公式的推导与简单应用，激发学生求知欲，鼓励学生大胆尝试，敢于探索、创新的学习品质。

重点

难点

重点   两角差余弦公式的探索和简单应用。

难点   探索过程的组织和引导。

教材

分析

    本节课的授课内容为人教版数学必修四第三章第一节的内容，教材中通过由特殊到一般的处理方式，采用两种方法推导出两角差的余弦公式，配以适当的练习加以巩固提升。

学情

分析

之前学习了三角函数的性质，以及平面向量的运算和应用，在此基础上，要考虑如何利用任意角的正弦余弦值来表示，牢固的掌握这个公式，并会灵活运用公式进行下一节内容的学习。

教学

策略

学生自主探究 教师适当引导  自主性学习法 探究式学习法

教学

资源

多媒体课件、学案

教学

媒体

多媒体、电子白板

教学过程设计

教学环节

教师活动

学生活动

设计意图

创设

情景

揭示

课题

研探

新知

例题

详解

公式逆用活用

课堂

小结

以实际问题为背景素材（见课件）引入问题。并针对问题中的用计算器或不用计算器计算求值，以激发兴趣，导入课题。

问题：（1）能不能不用计算器求值 ： ， ，（2）

1.三角函数线法（由于时间及学生程度等问题限制，此部分内容留给学生课后探究）

问：①怎样作出角、、的终边。

②怎样作出角的余弦线OM

③怎样利用几何直观寻找OM的表示式。

2.向量法：

问：①结合图形，明确应选哪几个向量，它们怎么表示？

②       怎样利用向量数量积的概念和计算公式得到结果。

③       对探索的过程进一步严谨性的思考和处理，从而得到合理的科学结论。

建立单位圆

由向量数量积的概念,有

由向量数量积的坐标表示,有

因为 、、都是任 意 角,所以也是任意角,但由诱导公式以总可找到一个，使得 。

于是对于任意角、都有     

例1.  利用差角余弦公式求的值

解法1：

解法2：

课堂训练1：

公式逆用

课堂训练

公式活用

课堂训练

1.两角差的余弦公式：                              

2.已知一个角的正弦（或余弦）值，求该角的余弦（或正弦）值时, 要注意该角所在的象限，从而确定该角的三角函数值符号.

3.在差角的余弦公式中， 既可以是单角，也可以是复角，运用时要注意角的变换，同时，公式的应用具有灵活性，解题时要注意正向、逆向和变式形式的选择。

回答老师提出的问题，可以小组合作交流。

尝试做出终边，及角的余弦线OM

小组探究明确应选择的向量，如何表示。思考如何将向量与两角差的余弦联系在一起。

让学生独立完成，注意引导学生多方向、多维度思考问题

学生自行解决问题

学生自主回顾本节课所学内容

由给出的背景素材，使学生感受数学源于生活，又应用于生活，唤起学生解决问题的兴趣，和抛出新知识引起学生的疑惑，在兴趣和疑惑中，激发学生的求知欲，引导学习方向。

让学生经历利用向量知识解决一个数学问题的过程，体会向量方法解决数学问题的简洁性。

通过这几个例题与训练题使学生初步掌握两角差的余弦公式的简单应用。      

进一步加深学生对公式的理解和应用，体验公式既可正用、逆用，还可变用.还可使学生掌握“变角”和“拆角”的思想方法解决问题，培养了学生的灵活思维品质，提高学生的数学交流能力，促进思维的创新。

让学生通过小结，反思学习过程，加深对公式的理解。

板书

设计

两角差的余弦公式

方法1：                      例1：                      小结：

方法2：                      例2：                      作业：

公式：                        练习：

作业设计

校本作业+优化设计课后作业

教学反思

本节课中预设让学生自己用向量法推导出两角差的余弦公式，但在实际上课过程中发现操作起来有困难，所以课堂上是采取教师适当引导的方式，在教师的引导下学生一步一步地推导出公式，在例题的讲解中，对于公式的直接应用掌握的很好，对于逆用及变形则有一部分同学没有办法一下子转过弯来，需要通过后面一定量习题的操练来熟练掌握这一部分的内容，