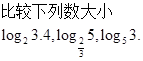课题

指数、对数函数单调性的应用

课型

习题课

章节

第二章第二节

年级班级

高一（1）班

教学

目标

1.       知识与技能：理解并掌握指数、对数函数的单调性及应用。

2.       过程与方法：通过同学们对指数函数单调性的研究，让学生总结与归纳；类比得到研究对数函数的方法，在过程中感悟数学思想方法。

3.       情感态度价值观：在学习过程中培养学生分析问题、解决问题、运用知识的能力。

重点

难点

重点：指数、对数单调性的应用，数学方法的总结、数学思想的感悟。

难点：结构化整体思维能力的培养。

教材

分析

指数、对数函数是基本初等函数之一，对它的定义、图像、性质等综合性应用的考查一直是高考的重点和热点。本节内容是在学习了指数、对数函数的图像与性质后，通过类比的方法对指数、对数函数的单调性做系统的归纳和小结，使学生对所学知识有个更系统的理解，并在教学过程中注重数学思想方法的渗透。

学情

分析

在前面学习了函数单调性、指数函数及对数函数的基础，让学生通过类比的方法将指数函数、对数函数的单调性进行归纳，老师教学生结构，学生运用结构，有利于直观认识的形成。

教学

策略

结构化教学、探究学习法

教学

资源

课件、学生作业

教学

媒体

电脑、实物投影仪

教学过程设计

教学环节

教师活动

学生活动

设计意图

活动1：

（表1）

活动2：

（表2）

活动3：

（表3）

拓展思考：

课堂小结：

1.请同学们仔细观察表1左侧的所给的数，它们在形式有什么共同点？

2.对于它由哪些要素构成？

3.再仔细观察这三组题中指数与底数的特点，思考我们该如何对这三组题进行归类？

4.对于第一组题，根据学生获得的方法总结，进一步让学生复习巩固单调性定义、指数函数的单调性，对数函数的单调性。

5.对于第一组题目中对数比较大小采用的方法一样吗？大家想想，在这组题中体现了哪些数学思想与方法？

6.请同学们类比第一组题目，完成剩下的表格。

探究1：已知，试确定m和n的大小关系。

探究2：

1.在求指数函数值域时我们用到的是什么方法？

2.探究活动3：

（1）根据前面的学习你能否将第一题中的指数函数一般化?请算一算情况怎么样.

（2）如果题目增加条件变为：上的最大值比最小值大的值。

（3）如果将指数函数改成对数函数，你会做吗？大家试试看！如果如果题目不能做，该如何改进？

3.在这整个过程中体现了哪些数学思想与方法？

1.根据前面的学习请同学们完成表3，四人小组讨论，学生作业展示。

2.进一步复习函数单调性定义的变形2.

3.探究活动4：

(1)如果题目换成：该如何做？

(2)你能将指数不等式变为对数不等式吗？都能算吗？如果不能你可以怎么改进？在解的过程中要注意什么？

若不等式（）在区间恒成立，求实数的取值范围。

类比：若不等式（）在区间恒成立，求实数的取值范围。

1.指数、对数函数单调性应用在哪些方面？

2.我们可以发现研究这些问题的常用方法有哪些？

3.这节课你学到了哪些数学思想与方法？

它们都形如

学生可以通过观察发现由底数和指数这两个要素组成。

可以分为三类：底数相同、指数不同；底数不同，指数相同；底数不同，指数不同.

小组讨论，展示作业。

小组讨论，学生回答。

小组讨论、学生回答、作业展示

小组讨论、学生回答、作业展示

学生回答、作业展示

从构成要素出发，引入比较大小的分类，比较自然、易于学生理解。

培养学生归纳能力。将所学知识回归概念、定义。

注重数学思想、方法的培养。引导学生用类比的方法研究对数比较大小。

学以致用。

从特殊到一般，化难为易，将未知转化为已知。

产生认知冲突，引入新的方法。

题目层层深入，前面的题目为后面的题目起铺垫作用，化难为易。

注重数学思想方法的总结。

学以致用。注重培养学生发散思维的能力。

注重学生能力的提升。

板书设计

1.       函数的单调性定义；

2.       指数、对数函数图像。

作业设计

《名校学案》第43-45页

教学反思

1.注重数学思想方法的渗透；2.利用表格归纳知识清晰明了；3.利用类比法教学；4.通过探究性问题培养学生分析问题的能力。